ACTIVIDAD 2

                                    GLOSARIO

Instrucciones cada uno de los siguientes puntos debe ser consultado en al menos dos fuentes bibliográficas, contar con al menos una imagen que sea de utilidad para explicar, y al final de glosario debe aparecer las bibliografías consultadas.

1)  Punto.

El Punto se define como un elemento geométrico que no tiene longitud, anchura, ni altura; se asemeja a la huella dejada por un alfiler. Este solo ocupa un lugar en el espacio.

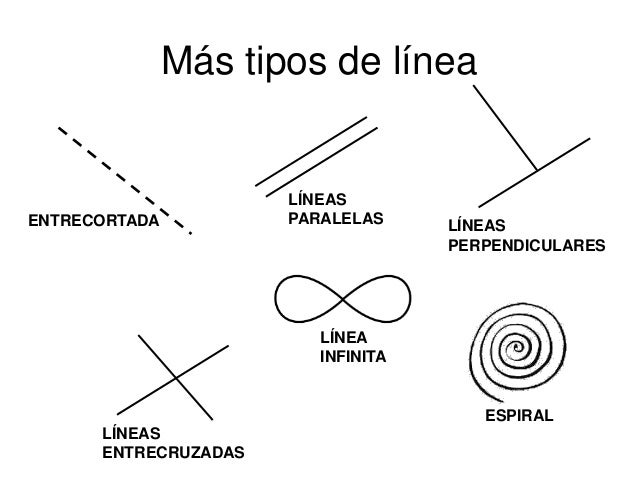
2) Linea

 Esta formada por una sucesión de puntos muy unidos, tan unidos que la percepción visual indicará que se trata de un trazo continuo, sin embargo en términos geométricos es esa la definición correcta, se trata pues de que a linea contiene una cantidad infinita de puntos. Una línea cualquiera aun con dimensiones ya establecidas, puede contener infinitos puntos, ya que la esta unión de punto sin dimensión alguna son incontables.

3)  Línea recta.

En geometría euclidiana, la recta o la línea recta es una línea que se extiende en una misma dirección por lo tanto tiene una sola dimensión y contiene un número infinito de puntos. Dicha recta también se puede describir como una sucesión continua de puntos extendidos en una sola dirección.

4)  Semirrecta.

Una SEMIRRECTA  es  una secuencia  de  puntos  que  se  

prolonga en  un  solo  sentido y  tiene  un  punto de  origen.

En este  caso se  llama  A. Pero no  tiene punto final.

5)  Segmento de línea recta.

SEGMENTO es una  secuencia  de  puntos de

rectilíneos que  tiene  un punto de origen  y  un punto

final. En  este  caso se  origina  en  A y  finaliza  en  B.

6)  Ángulo.

 hace referencia a una figura de la geometría que se forma a partir de dos rectas que se cortan entre sí en una misma superficie. También puede decirse que un ángulo está formado por dos semirrectas que comparten un mismo vértice.

7)  Sistemas de medición de ángulos (Grados (decimal y sexagesimal) y Radianes). Como convertir de grados a radianes y de grados decimales a grados sexagesimales.

8)  Una clasificación de ángulos según su medida es:
    a)     Ángulo recto.
Ángulo recto: Mide 90° y sus lados son siempre perpendiculares entre sí.

  
  b)     Ángulo agudo.
Ángulo agudo: Mide menos de 90° y más de 0 °.

    
c)     Ángulo obtuso.
Ángulo obtuso: Mayor que 90° pero menor que 180°.

    
d)     Ángulo llano.
Ángulo llano: Mide 180°. Igual que si juntamos dos ángulos rectos.

    
e)     Ángulo entrante o cóncavo

El ángulo cóncavo es un ángulo que oscila entre los 180º y los 360º

     
f)     Ángulo perígono.

Es el ángulo de una circunferencia completa, o el haz completo de semirrectas; aquel que mide 360º en el sistema sexagesimal o 400g en el centesimal.

9)  Otra clasificación de los ángulos según su posición es:

    
a)     Opuestos por el vértice.
Se denominan Ángulos opuestos por el vértice cuando los lados de uno son semi rectas contrarias a los lados del otro. Los ángulos opuestos al vértice tienen como propiedad que “todos los ángulos opuestos por el vértice son iguales”.

   b)     Adyacentes.
Un ángulo es considerado adyacente cuando tienen un ángulo y un vértice en común, a la vez que sus demás lados son semirrectas contrarias, a su vez los ángulos adyacentespueden ser consecutivos y suplementarios, puesto que al unirse se asemejan a un ángulollano, sin tener un punto interior en común.

   c)     Complementarios
Los ángulos complementarios son los que sumados son iguales al valor de un ángulo recto, es decir, un ángulo de 90 grados. En caso de que los lados que son comunes estén uno al lado del otro (consecutivos) el ángulo recto se apreciara, sin embargo no necesariamente los ángulos complementarios tienen que ser consecutivos, basta que la suma de ambos sea de 90º. Por ejemplo los dos ángulos no rectos de un triángulo rectángulo, son complementarios y no son consecutivos.

    
d)     Suplementarios.
Los ángulos suplementarios son aquellos que en par suman 180 grados. A diferencia de los ángulos complementarios que forman 90 grados. Siguiendo la misma propiedad y fórmula de los que se complementan entre sí, un ángulo que tenga menos de 180 grados le corresponderá un ángulo que lo suplementa según la fórmula A (ángulo suplementario)= 180° menos (-) el ángulo que necesita suplemento. Ejemplo: A = 180° – 150° = 30°.

10)  Triángulo



Son polígonos de tres lados.

11)  Clasificación de los triángulos por
sus lados.

    1) triángulos equiláteros.

Son los triángulos cuyos tres lados son iguales.

2) triángulos isósceles.

Triangulo que tiene 2 lados iguales y uno diferente.

3) triángulos escalenos.

Triángulos cuyo lados son deferentes.

12)  Clasificación de los triángulos por sus ángulos.

• Triángulo obtusángulo: es el que tiene un ángulo obtuso (mayor que 90°).
   
• Triángulo acutángulo: es el que tiene tres ángulos agudos (menores que 90°).
   
• Triángulo rectángulo: es el que tiene un ángulo recto (de 90°).

13)  Rectas y puntos notables en el triángulo.

14)  Polígonos regulares e irregulares

15)  Propiedades de los polígonos:

a.    Suma de los ángulos interiores

b.    Número de triángulos que se forman en el interior.

16)  Perímetro y Área de Polígonos.

17) Fórmula de Herón
INFORMACIÓN AQUÍ.

18)  Circunferencia. Rectas y segmentos en:

19)  Ángulos en una circunferencia.

Bibliográfias Consultadas:

//www.aulafacil.com/cursos/l11142/ciencia/matematicas/geometria/clasificacion-de-los-triangulo-segun-sus-ladoshttp:
https://www.thatquiz.org/es/previewtest?T/S/J/I/32831341886500
http://trazoide.com/angulo-perigonal/
https://www.smartick.es/blog/matematicas/recursos-didacticos/angulos-i/
(07/03/2018).